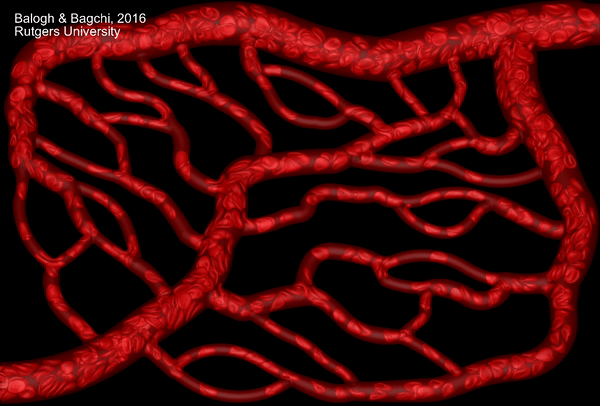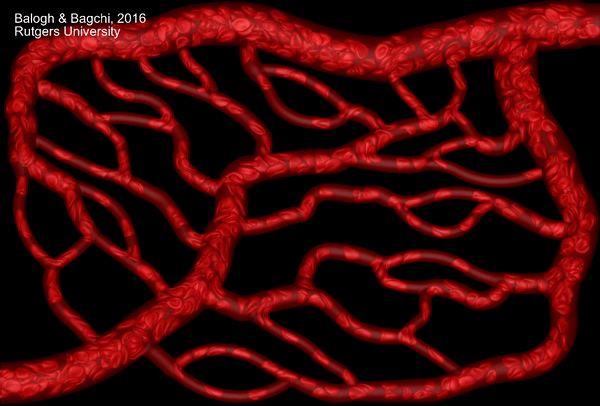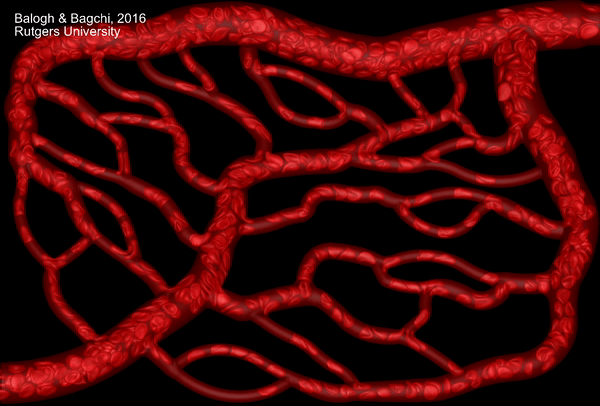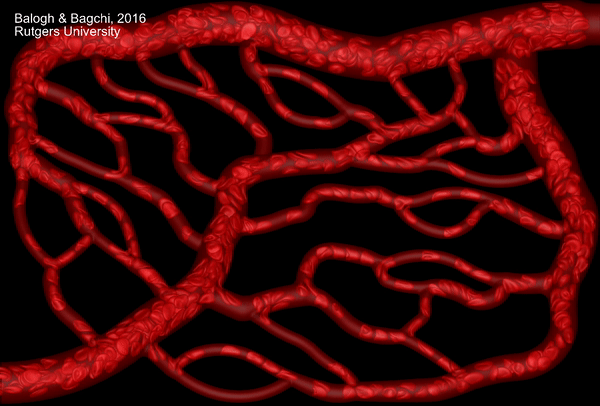
Despite a significant progress in the past decade, high-fidelity computational modeling of cellular-scale blood flow continues to pose new challenges. Red blood cells are extremely deformable particles. Numerical modeling of large deformation of red blood cells in 3D is a challenging task. In addition, whole blood is a poly-disperse suspension of red blood cells, white blood cells and platelets. Most computational modeling studies have considered flow of blood cells in simple geometry, such as parallel plate-like geometry or in straight tubes. In contrast, physiologically realistic blood vessels are highly complex in gemetry. The vessels continually bifurcate and merge, and they are often winding. These vessels together form the so-called microvascular network. The architecture of the netwrok is different depending on which organ or tissue is considered. Certainly, computational models for blood flow in straight tubes are not sufficient to address cell motion in such geometrically complex microvascular networks. The model must address large deformation of individual blood cells, and the geometric complexity of the network architecture.
We have developed a high-fidelity, state-of-the-art modeling tool to simulate flow of many blood cells in physiologically realistic and geometrically complex microvascular networks. The model incorporates a sharp-interface (ghost-node) immersed-boundary method to handle the geometric complexity, a finite-volume method for fluid flow, a finite-element model for cell deformation, and a front-tracking method for cell--flow coupling. The animation above is from one such simulation. The network is obtained following published in vivo images which are digitally rendered for our simulations.
Related publications:
- Balogh, P. and Bagchi, P. 2017. Direct simulation of cellular-scale blood flow in microvascular networks. (Under consideration).
- Balogh, P. and Bagchi, P. 2017. A computational approach to modeling cellular-scale blood flow in complex geometry. Journal of Computational Physics, 334, 280-307.
Here is another animation from our simulations:
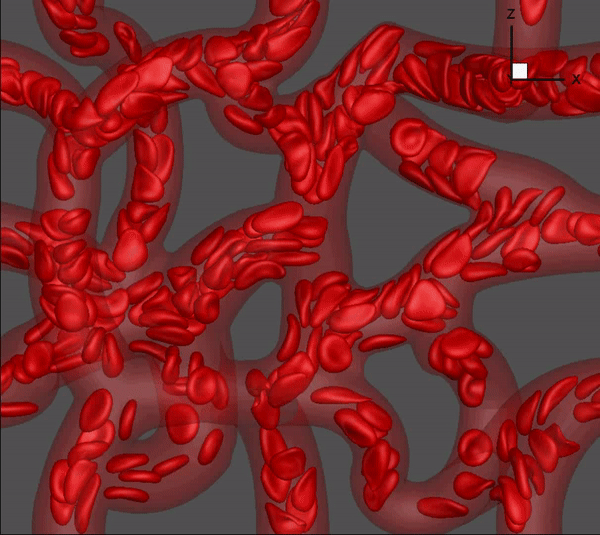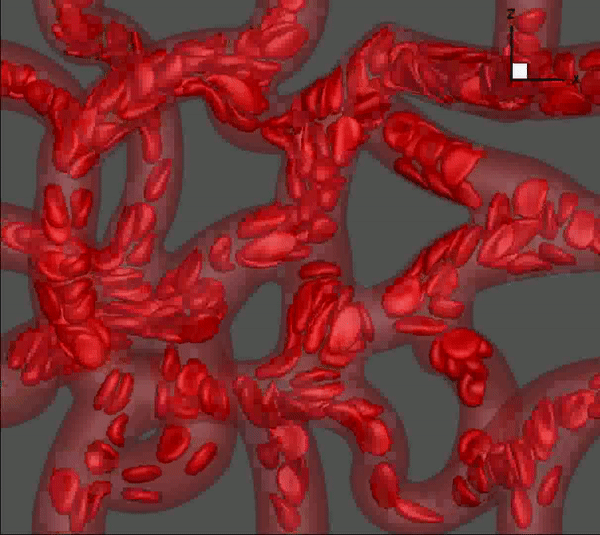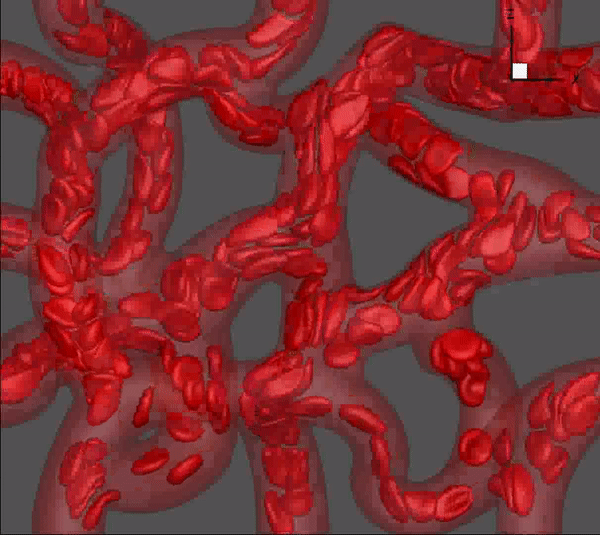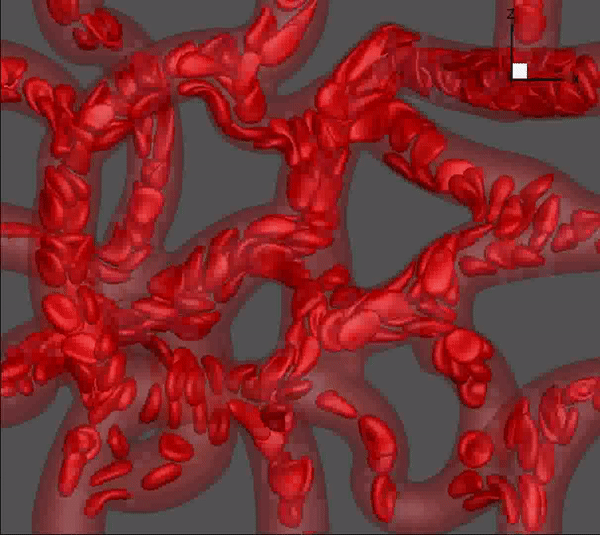Balogh & Bagchi, 2017, J. Comput. Phys.
Other problems of interest:
Microvascular stenosis
One of our research interest is to understnd the microscale mechanism of vascular disease. Towards that end, we recently considered a simulation study of flow of deformable blood cells in microvascular stenosis. We observe that the Fahraeus-Lindqvist effect is significantly enhanced due to the interaction of the stenosis and flowing blood cells. Below is an animation from our simulations:
Vahidkhah, Balogh, & Bagchi. 2016. Sci. Report.
Related publications:
- Vahidkhah, K., Balogh, P., and Bagchi, P. 2016. Flow of red blood cells in stenosed microvessels. Scientific Reports (published by Nature publications). 6, 28194.
Below is another animation from our simulations on flow of blood cells in a microvessel:
